Lecture 1 && Lecture 2:机器学习/深度学习基本概念简介

Lecture 1: Introduction of ML/DL

机器学习基本概念简介

Machine Learning $\approx$ Looking for Function——机器学习就是让机器（程序）具备找一个函数的能力。

Different types of Funtions：

• Regression（回归）——连续。最终得到标量（scalar）

• Classification（分类）——离散。得到一个选择（options/classes）

• 除此两大任务外，还有Structured Learning：让机器不仅学会分类或者实现预测任务，而且可以创造特定的“有结构”的物体，譬如文章、图像等。

机器学习如何找到这个函数？（三个步骤）

• Function with Unknown Parameters：

  譬如$y = b + wx_1$，该假设方程是基于domain knowledge（领域知识）各种定义：

  • Model：带有未知的参数(Parameters)的函数（function）。
  • $x_1$是feature，$w$是weight，$b$是bias，后两个未知参数基于数据(data)学习得到。

• Define Loss from Training Data：

  • Loss，即损失函数，一个仅带有函数未知的参数的方程，记作$L(b,w)$
  • Loss的值体现了函数的一组参数的设定的优劣
  • 通过训练资料来计算loss = |估测值 - 真正值|，Label指的就是正确的数值$\hat{y}$，$e_i = |y - \hat{y}|,i = 1,2,..,n$，所以。Loss：$L = \Large\frac{1}{N}\sum_n^{i=1}e_i$。其中，差值$e$的有不同的计算方法，如上采用直接做差得绝对值（Mean Absolute Error：MAE），还有$e = (y-\hat{y})^2$，即Mean Square Error：MSE。选择哪一种方法衡量$e$取决于我们的需求以及对于task的理解。
  • 我们枚举不同参数组合（$w,b$）通过计算Loss值画出等高线图：Error Surface
  • 如果$y$和$\hat{y}$都是概率==>Cross-entropy：交叉熵
  • loss函数自定义设定，如果有必要的话，loss函数可以output负值

• Optimization

  • $w^,b^ = arg\space \underset{w,b}{min}L $

  • 为了实现上述任务（找到$w,b$使得$L$最小）,通常采用梯度下降法（Gradient Descent）。譬如：隐去其中一个参数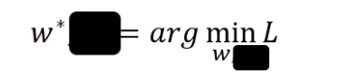从而得到一个$w-Loss(L)$的数值曲线，记作$L(w)$

    • 随机选取一个初始值：$w_0$

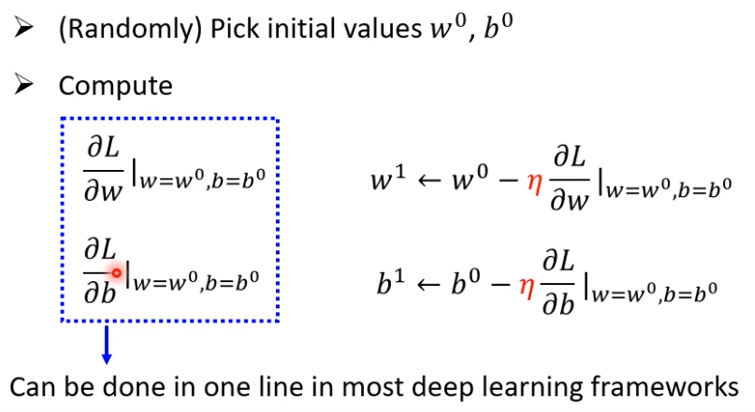
    • 计算：$\Large \frac{\partial L}{\partial w}|_{w=w_0}$，该点位置在Error Surface的切线斜率：若负值（Negative），左高右低=>$w$右移$\eta$使得$Loss$变小；若正值（Positive），左底右高=>$w$左移$\eta$使得$Loss$变小。斜率大=>步伐$\eta$跨大一些；斜率小=>步伐$\eta$跨小一些。$w_1 \leftarrow w_0 - \eta \large \frac{\partial L}{\partial w}|_{w=w_0}$

      $\eta$ : learning rate学习率，属于hyper parameters：超参数，自己设定，决定更新速率。

    • 不断迭代更换$w$

      “假”问题：囿于局部最优解local minimal，忽略了实际的最优解global minima（不过并非梯度下降法的真正痛点）

  • 类似的，将单参数随机梯度下降法推广到两参数上：$w^,b^ = arg\space \underset{w,b}{min}L $

    

    确定更新方向：$(- \eta \large \frac{\partial L}{\partial w},- \eta \large \frac{\partial L}{\partial b})$，$\eta$为学习率

    总结来说，基本步骤如下

以上三步是机器学习最为基本的框架。基于此，还需要理解任务，摸索数据变化规律==>修改模型（model）

---

深度学习基本概念简介

在以上基本步骤上进行深层的探讨。

Step 1：定义含有未知参数的函数

线性函数被首先考虑。线性模型（Linear Model）过于简单，无论参数组合如何可能总是无法完全拟合任务的Model，这里说明Linear Model具有severe limitation，这种局限被称之为Model Bias。于是我们需要更为复杂的函数。

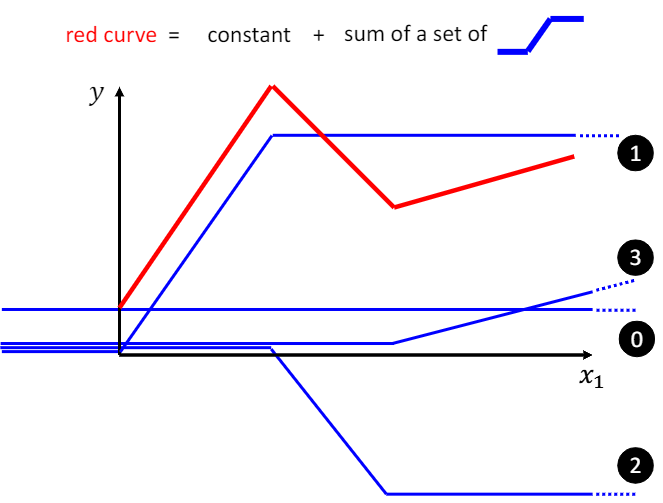
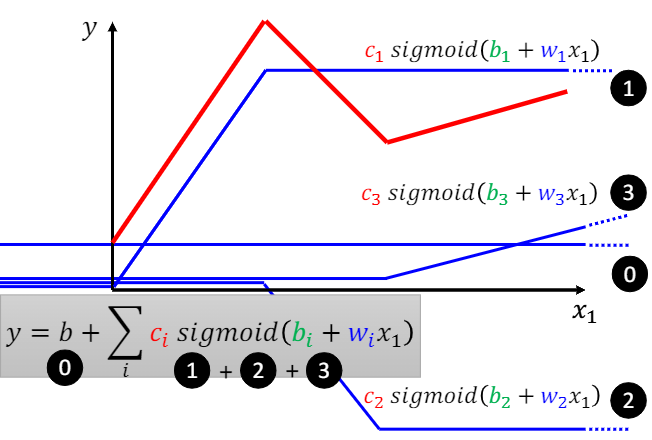
这里类似于使用阶跃函数的组合来表示分段函数，red curve= 1 + 2 + 3 + 0（常数项）,这里归纳出一个常见的结论：分段函数$All\space Piecewise\space Linear\space Curves = constant$(常数项) +

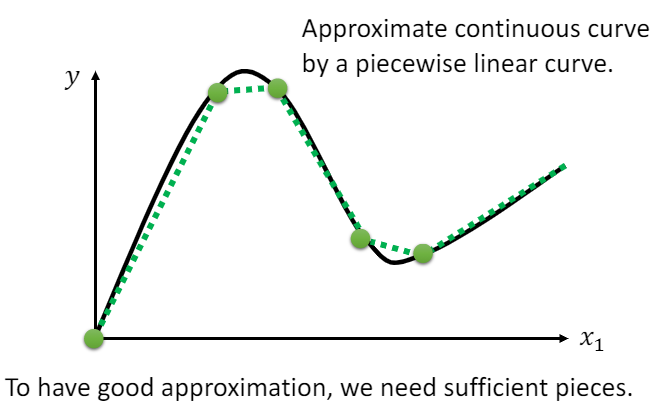
那么，对于$Beyond\space Piecewise\space Linear\space Curves$（这也是我们常见的一般函数的曲线），我们使用许多多不一样的小线段去“逼近”连续的这条曲线：

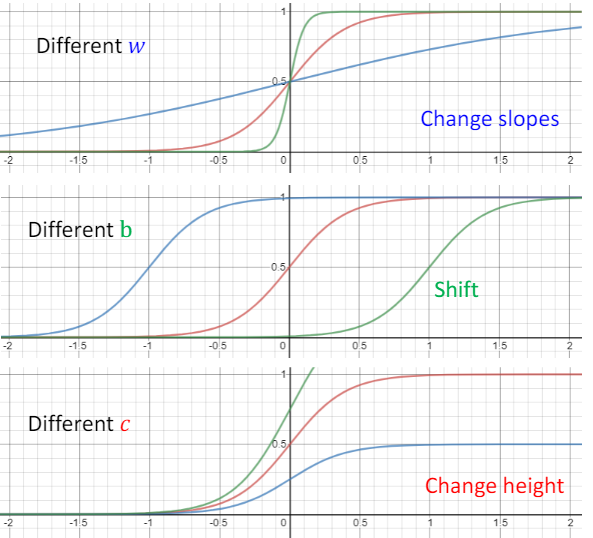
为了表示这样一个蓝色的函数（小线段）（被称之Hard Sigmoid），这里用一个常见的指数函数来逼近——Sigmoid Function

$$y = c \large \frac{1}{1 + e^{-(b+wx_1)}}= c·sigmoid(b+wx_1)$$

通过调整$w,b,c$，一组参数组合可以得到不同逼近的小线段👇

这个引入超级棒！！由上易知，一个连续的复杂的函数曲线可以被分解成许多离散的小线段（Hard Sigmoid）和一个常数项的线性相加，然后每个小线段被一个三参数的Sigmoid Function所逼近。下图的函数曲线可以表示为一个含有10个未知参数的mode：

从而，可以产生一个从简单->复杂、单一->多元的函数模式。新的模型包含更多的特征。

$$y=b+wx_1 \Rightarrow y = b + \underset{i}{\sum}c_i sigmoid(b_i+w_ix_1)$$

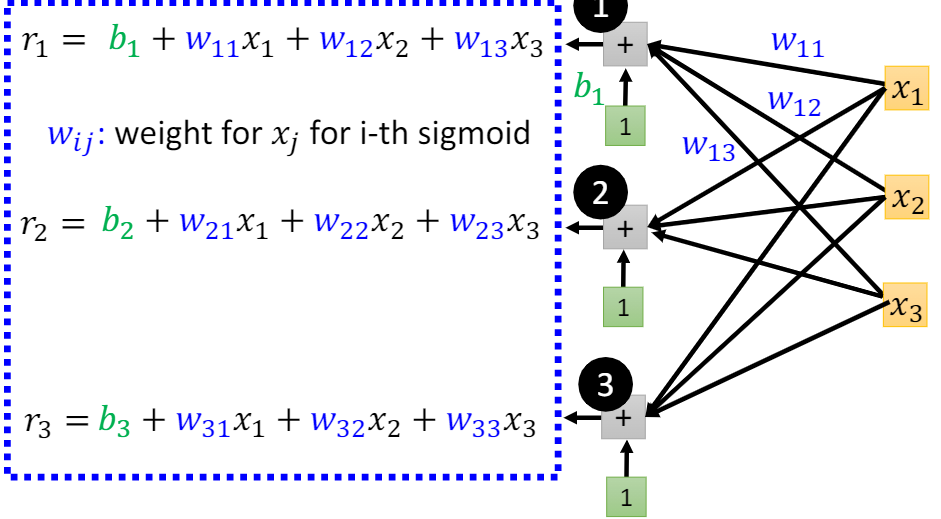
由（2）式，考虑到多特征因素，进一步扩展得

$$y = b + \underset{j}{\sum}w_jx_j \Rightarrow y = b + \underset{i}{\sum}c_i sigmoid(b_i+\underset{j}{\sum}w_{ij}x_1)$$

其中$i$表示$i^{th}$个$Sigmoid$函数（模型的基函数个数），$x_j$表示一个函数中不同的特征或者预测的数据长度，，$w_j$表示对应特征权值。

总结：在通用的机器学习教程中，$sigmoid$函数普遍被视作一款常见的激活函数，在本课程中，从代表任务模型的非线性函数出发—>极限：分段的线性函数组合—>不同性质/特征的$sigmoid$函数逼近小分割的线性函数。如上图所示，我们有三个激活函数（$sigmoid \space function$）以及输出的一个方程组（矩阵/向量相乘表示），这里基本上可以视为一个具有三个神经元的全连接的一层神经网络。

$$[r_1,r_2,r_3]^T = [b_1,b_2,b_3]^T + \begin{bmatrix}w_{11},w_{12},w_{13}\\w_{21},w_{22},w_{23}\\w_{31},w_{32},w_{33} \end{bmatrix}·[x_1,x_2,x_3]^T$$

总之，

$$r = \mathbb {b} +W·\mathbb{x}$$

接下来，将该方程组$r$通过激活函数输出向量$a$，这里

$$a = \sigma(r)$$

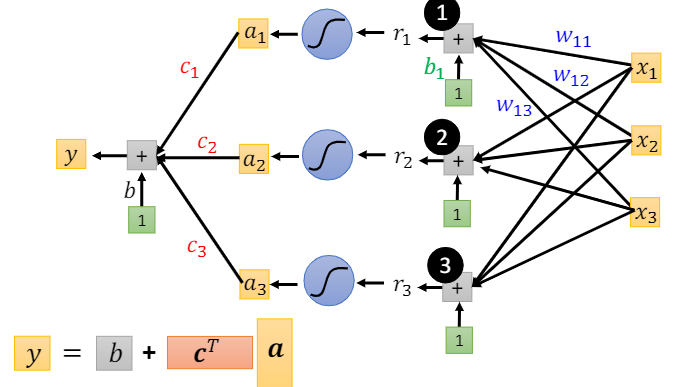
由(5)、(6)得

$$由 a= \sigma(\mathbb{b} + W·\mathbb{x}): \\\Rightarrow y = b + [c_1,c_2,c_3]·\sigma(\mathbb{b} + W·\mathbb{x}) \Rightarrow y = b + \mathbb{c}^T\sigma(\mathbb{b} + W·\mathbb{x})$$

注意，$\sigma$中的$\mathbb{b}$是向量，外面的$b$是数值，结果$y$也是数值（标量）。

在该例子中，$\mathbb{x}$表示特征，$\mathbb{c}、\mathbb{b}、W、b$为未知参数。为了把未知参数统一起来处理，我们进行如下泛化，比方说，$\theta_1 = [c_1,b_1,w_{11},w_{12},w_{13},b]^T$

$\mathbb{\theta}$是一个很长的向量，里面的第一个向量为$\theta_1$，以此类推。只要是未知参数都统称在$\theta$内。

在参数很少的时候，可以直接穷举参数组合，寻找最优解；但是当机器学习问题中的参数较多时，梯度下降法更为合理。隐含层神经元节点个数（$sigmoid$函数个数）自己决定，其本身个数数值也为超参数之一。

Step 2：确定loss函数

• loss是一个未知参数的函数：$L(\mathbb{\theta})$
• loss衡量一组参数值表示模型效果优劣

同以上介绍的步骤无区别。

Step 3：Optimization

新模型的的optimization步骤和之前介绍的无任何区别。对于$\mathbb{\theta}=[\theta_1,\theta_2,\theta_3…]^T$

• 随机选取初始值$\mathbb{\theta}^0$，gradient梯度记为$\large\mathbb{\mathcal{g}}=[\frac{\partial L}{\partial \theta_1}_{|\mathbb{\theta}=\mathbb{\theta}^0},\frac{\partial L}{\partial \theta_2}_{|\mathbb{\theta}=\mathbb{\theta}^0},…]^T$，可简化为$\mathbb{\mathcal{g}}=\nabla L(\mathbb{\theta}^0)$向量长度=参数个数。

• 更新参数👇($\eta$当然是学习率啦)

  $$\mathbb{\theta}=[\theta_1^1,\theta_2^1,...]^T \leftarrow \mathbb{\theta}=[\theta_1^0,\theta_2^0,...]^T - [\textcolor{red}\eta\frac{\partial L}{\partial \theta_1}_{|\mathbb{\theta}=\mathbb{\theta}^0},\textcolor{red}\eta\frac{\partial L}{\partial \theta_2}_{|\mathbb{\theta}=\mathbb{\theta}^0},...]^T \\ \mathbb{\theta}^1 \leftarrow \mathbb{\theta}^0 - \textcolor{red}\eta \mathbb{\mathcal{g}}$$

  不断迭代$\mathbb{\theta}^2 \leftarrow \mathbb{\theta}^1 - \textcolor{red}\eta \mathbb{\mathcal{g}},\mathbb{\theta}^3 \leftarrow \mathbb{\theta}^2 - \textcolor{red}\eta \mathbb{\mathcal{g}},…$，直到找到不想做或者梯度最后是zero vector（后者不太可能）。

实际上在做梯度下降的时候，我们要把数据$N$分成若干Batch（称之为批量）,如何分？随便分。原先是把所有data拿来算一个loss，现在是在一个Batch上算loss，那么对于$B_1,B_2,…$我们可以得到$L^1,L^2,…$

把所有batch算过一次，称之为一个epoch：1 epoch = see all the batches once。以上即为批量梯度下降。注意区别：一次update指的是每次更新一次参数，而把所有的Batch看过一遍则是epoch。

另外，Batch Size大小也是一个超参数。

对模型做更多的变形：

$Sigmoid \rightarrow ReLU$：Rectified Linear Unit（ReLU）：$c·max(0,b+wx_1)$曲线。不同的是，我们需要两个$ReLU$曲线才能合成一个Hard Sigmoid函数曲线（蓝色的小线段）。无论是$Sigmoid$还是$ReLU$都是激活函数（Activation Function）。

上面的长篇大论仅仅讲述了一层神经网络是如何搭建的，那么多层神经网络的耦合（或者是逐步构建隐藏层）$\rightarrow$深度学习（Deep Learning）。老师表示这里的层数也是个超参数哦。层数越多，参数越多。

同一层好多个激活函数（Neruon）就是一个hidden layer，多个hidden layer组成了Neural Network。这一整套技术就是deep learning。

之后的神经网络层数越来越多（AlexNet、GoogLeNet等等）那么为什么是深度学习而不是宽（肥）度学习？另外，当层数变多了，就会overfitting（过拟合）。这些是我们之后课程要讨论的问题。